Now that we know that the abstract syntax tree is important (but not necessarily intimidating!), we can start to dissect it a tiny bit more. An interesting aspect about how the AST is constructed has to do with the nodes of this tree.

The image below exemplifies the anatomy of a single node within an abstract syntax tree.

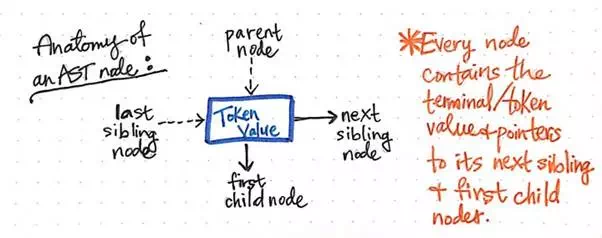
The anatomy of an AST node.

We’ll notice that this node is similar to others that we’ve seen before in that it contains some data (a token and its value). However, it also contains some very specific pointers. Every node in an AST contains references to its next sibling node, as well as its first child node.

For example, our simple expression of 5 + (1 x 12) could be constructed into a visualized illustration of an AST, like the one below.

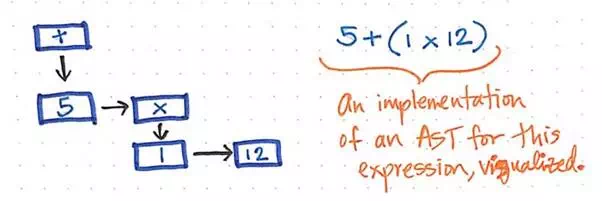
A simplified visualization of our AST expression.

We can imagine that reading, traversing, or “interpreting” this AST might start from the bottom levels of the tree, working its way back up to build up a value or a return result by the end.

It can also help to see a coded version of the output of a parser to help supplement our visualizations. We can lean on various tools and use preexisting parsers to see a quick example of what our expression might look like when run through a parser. Below is an example of our source text, 5 + (1 * 12), run through Esprima, an ECMAScript parser, and its resulting abstract syntax tree, followed by a list of its distinct tokens.

A code visualization of our AST expression, using JavaScript.

In this format, we can see the nesting of the tree if we look at the nested objects. We’ll notice that the values containing 1 and 12 are the left and rightchildren, respectively, of a parent operation, *. We’ll also see that the multiplication operation (*) makes up the right subtree of the entire expression itself, which is why it is nested within the larger BinaryExpression object, under the key "right". Similarly, the value of 5 is the single "left" child of the larger BinaryExpression object.

Building an AST can be complex sometimes.

The most intriguing aspect of the abstract syntax tree is, however, the fact that even though they are so compact and clean, they aren’t always an easy data structure to try and construct. In fact, building an AST can be pretty complex, depending on the language that the parser is dealing with!

Most parsers will usually either construct a parse tree (CST) and then convert it to an AST format, because that can sometimes be easier — even though it means more steps, and generally speaking, more passes through the source text. Building a CST is actually pretty easy once the parser knows the grammar of the language it’s trying to parse. It doesn’t need to do any complicated work of figuring out if a token is “significant” or not; instead, it just takes exactly what its sees, in the specific order that it sees it, and spits it all out into a tree.

On the other hand, there are some parsers that will try to do all of this as a single-step process, jumping straight to constructing an abstract syntax tree.

Building an AST directly can be tricky, since the parser has to not only find the tokens and represent them correctly, but also decide which tokens matter to us, and which ones don’t.

In compiler design, the AST ends up being super important for more than one reason. Yes, it can be tricky to construct (and probably easy to mess up), but also, it’s the last and final result of the lexical and syntax analysis phases combined! The lexical and syntax analysis phases are often jointly called the analysis phase, or the front-end of the compiler.

The inner workings of the front-end of our compiler.

We can think about the abstract syntax tree as the “final project” of the front-end of the compiler. It’s the most important part, because its the last thing that the front-end has to show for itself. The technical term for this is called the intermediate code representation or the IR, because it becomes the data structure that is ultimately used by the compiler to represent a source text.