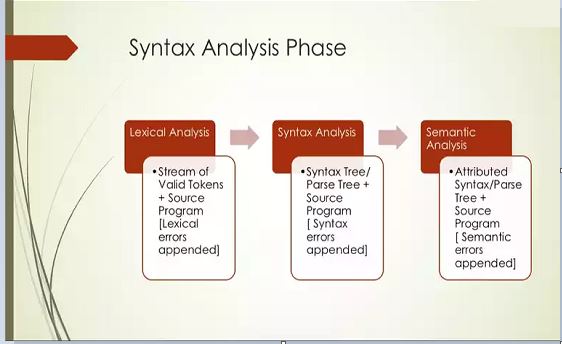
Syntax analysis or parsing is the second phase of a compiler. In this chapter, we shall learn the basic concepts used in the construction of a parser.
We have seen that a lexical analyzer can identify tokens with the help of regular expressions and pattern rules. But a lexical analyzer cannot check the syntax of a given sentence due to the limitations of the regular expressions. Regular expressions cannot check balancing tokens, such as parenthesis. Therefore, this phase uses context-free grammar (CFG), which is recognized by push-down automata.
CFG, on the other hand, is a superset of Regular Grammar, as depicted below:

It implies that every Regular Grammar is also context-free, but there exists some problems, which are beyond the scope of Regular Grammar. CFG is a helpful tool in describing the syntax of programming languages.
Context-Free Grammar
In this section, we will first see the definition of context-free grammar and introduce terminologies used in parsing technology.
A context-free grammar has four components:
· A set of non-terminals (V). Non-terminals are syntactic variables that denote sets of strings. The non-terminals define sets of strings that help define the language generated by the grammar.
· A set of tokens, known as terminal symbols (Σ). Terminals are the basic symbols from which strings are formed.
· A set of productions (P). The productions of a grammar specify the manner in which the terminals and non-terminals can be combined to form strings. Each production consists of a non-terminal called the left side of the production, an arrow, and a sequence of tokens and/or on- terminals, called the right side of the production.
· One of the non-terminals is designated as the start symbol (S); from where the production begins.
The strings are derived from the start symbol by repeatedly replacing a non-terminal (initially the start symbol) by the right side of a production, for that non-terminal.
Example
We take the problem of palindrome language, which cannot be described by means of Regular Expression. That is, L = { w | w = wR } is not a regular language. But it can be described by means of CFG, as illustrated below:
G = ( V, Σ, P, S )
Where:
V = { Q, Z, N }
Σ = { 0, 1 }
P = { Q → Z | Q → N | Q → ℇ | Z → 0Q0 | N → 1Q1 }
S = { Q }
This grammar describes palindrome language, such as: 1001, 11100111, 00100, 1010101, 11111, etc.
Syntax Analyzers
A syntax analyzer or parser takes the input from a lexical analyzer in the form of token streams. The parser analyzes the source code (token stream) against the production rules to detect any errors in the code. The output of this phase is a parse tree.

This way, the parser accomplishes two tasks, i.e., parsing the code, looking for errors and generating a parse tree as the output of the phase.
Parsers are expected to parse the whole code even if some errors exist in the program. Parsers use error recovering strategies, which we will learn later in this chapter.
Derivation
A derivation is basically a sequence of production rules, in order to get the input string. During parsing, we take two decisions for some sentential form of input:
- Deciding the non-terminal which is to be replaced.
- Deciding the production rule, by which, the non-terminal will be replaced.
To decide which non-terminal to be replaced with production rule, we can have two options.
Left-most Derivation
If the sentential form of an input is scanned and replaced from left to right, it is called left-most derivation. The sentential form derived by the left-most derivation is called the left-sentential form.
Right-most Derivation
If we scan and replace the input with production rules, from right to left, it is known as right-most derivation. The sentential form derived from the right-most derivation is called the right-sentential form.
Example
Production rules:
E → E + E
E → E * E
E → id
Input string: id + id * id
The left-most derivation is:
E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
E → id + id * id
Notice that the left-most side non-terminal is always processed first.
The right-most derivation is:
E → E + E
E → E + E * E
E → E + E * id
E → E + id * id
E → id + id * id
Parse Tree
A parse tree is a graphical depiction of a derivation. It is convenient to see how strings are derived from the start symbol. The start symbol of the derivation becomes the root of the parse tree. Let us see this by an example from the last topic.
We take the left-most derivation of a + b * c
The left-most derivation is:
E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
E → id + id * id
Step 1:
| E → E * E |  |
Step 2:
| E → E + E * E |  |
Step 3:
| E → id + E * E |  |
Step 4:
| E → id + id * E |  |
Step 5:
| E → id + id * id |  |
In a parse tree:
- All leaf nodes are terminals.
- All interior nodes are non-terminals.
- In-order traversal gives original input string.
A parse tree depicts associativity and precedence of operators. The deepest sub-tree is traversed first, therefore the operator in that sub-tree gets precedence over the operator which is in the parent nodes.
Ambiguity
A grammar G is said to be ambiguous if it has more than one parse tree (left or right derivation) for at least one string.
Example
E → E + E
E → E – E
E → id
For the string id + id – id, the above grammar generates two parse trees:

The language generated by an ambiguous grammar is said to be inherently ambiguous. Ambiguity in grammar is not good for a compiler construction. No method can detect and remove ambiguity automatically, but it can be removed by either re-writing the whole grammar without ambiguity, or by setting and following associativity and precedence constraints.
Associativity
If an operand has operators on both sides, the side on which the operator takes this operand is decided by the associativity of those operators. If the operation is left-associative, then the operand will be taken by the left operator or if the operation is right-associative, the right operator will take the operand.
Example
Operations such as Addition, Multiplication, Subtraction, and Division are left associative. If the expression contains:
id op id op id
it will be evaluated as:
(id op id) op id
For example, (id + id) + id
Operations like Exponentiation are right associative, i.e., the order of evaluation in the same expression will be:
id op (id op id)
For example, id ^ (id ^ id)
Precedence
If two different operators share a common operand, the precedence of operators decides which will take the operand. That is, 2+3*4 can have two different parse trees, one corresponding to (2+3)*4 and another corresponding to 2+(3*4). By setting precedence among operators, this problem can be easily removed. As in the previous example, mathematically * (multiplication) has precedence over + (addition), so the expression 2+3*4 will always be interpreted as:
2 + (3 * 4)
These methods decrease the chances of ambiguity in a language or its grammar.
Left Recursion
A grammar becomes left-recursive if it has any non-terminal ‘A’ whose derivation contains ‘A’ itself as the left-most symbol. Left-recursive grammar is considered to be a problematic situation for top-down parsers. Top-down parsers start parsing from the Start symbol, which in itself is non-terminal. So, when the parser encounters the same non-terminal in its derivation, it becomes hard for it to judge when to stop parsing the left non-terminal and it goes into an infinite loop.
Example:
(1) A => Aα | β
(2) S => Aα | β
A => Sd
(1) is an example of immediate left recursion, where A is any non-terminal symbol and α represents a string of non-terminals.
(2) is an example of indirect-left recursion.

A top-down parser will first parse the A, which in-turn will yield a string consisting of A itself and the parser may go into a loop forever.
Removal of Left Recursion
One way to remove left recursion is to use the following technique:
The production
A => Aα | β
is converted into following productions
A => βA’
A’=> αA’ | ε
This does not impact the strings derived from the grammar, but it removes immediate left recursion.
Second method is to use the following algorithm, which should eliminate all direct and indirect left recursions.
START
Arrange non-terminals in some order like A1, A2, A3,…, An
for each i from 1 to n
{
for each j from 1 to i-1
{
replace each production of form Ai ⟹Aj휸
with Ai ⟹ δ1휸 | δ2휸 | δ3휸 |…| 휸
where Aj ⟹ δ1 | δ2|…| δn are current Aj productions
}
}
eliminate immediate left-recursion
END
Example
The production set
S => Aα | β
A => Sd
after applying the above algorithm, should become
S => Aα | β
A => Aαd | βd
and then, remove immediate left recursion using the first technique.
A => βdA’
A’ => αdA’ | ε
Now none of the production has either direct or indirect left recursion.
Left Factoring
If more than one grammar production rules has a common prefix string, then the top-down parser cannot make a choice as to which of the production it should take to parse the string in hand.
Example
If a top-down parser encounters a production like
A ⟹ αβ | α휸 | …
Then it cannot determine which production to follow to parse the string as both productions are starting from the same terminal (or non-terminal). To remove this confusion, we use a technique called left factoring.
Left factoring transforms the grammar to make it useful for top-down parsers. In this technique, we make one production for each common prefixes and the rest of the derivation is added by new productions.
Example
The above productions can be written as
A => αA’
A’=> β | 휸 | …
Now the parser has only one production per prefix which makes it easier to take decisions.
First and Follow Sets
An important part of parser table construction is to create first and follow sets. These sets can provide the actual position of any terminal in the derivation. This is done to create the parsing table where the decision of replacing T[A, t] = α with some production rule.
First Set
This set is created to know what terminal symbol is derived in the first position by a non-terminal. For example,
α → t β
That is α derives t (terminal) in the very first position. So, t ∈ FIRST(α).
Algorithm for calculating First set
Look at the definition of FIRST(α) set:
- if α is a terminal, then FIRST(α) = { α }.
- if α is a non-terminal and α → ℇ is a production, then FIRST(α) = { ℇ }.
- if α is a non-terminal and α → 휸1 휸2 휸3 … 휸n and any FIRST(휸) contains t then t is in FIRST(α).
First set can be seen as:

Follow Set
Likewise, we calculate what terminal symbol immediately follows a non-terminal α in production rules. We do not consider what the non-terminal can generate but instead, we see what would be the next terminal symbol that follows the productions of a non-terminal.
Algorithm for calculating Follow set:
· if α is a start symbol, then FOLLOW() = $
· if α is a non-terminal and has a production α → AB, then FIRST(B) is in FOLLOW(A) except ℇ.
· if α is a non-terminal and has a production α → AB, where B ℇ, then FOLLOW(A) is in FOLLOW(α).
Follow set can be seen as: FOLLOW(α) = { t | S *αt*}
Limitations of Syntax Analyzers
Syntax analyzers receive their inputs, in the form of tokens, from lexical analyzers. Lexical analyzers are responsible for the validity of a token supplied by the syntax analyzer. Syntax analyzers have the following drawbacks –
- it cannot determine if a token is valid,
- it cannot determine if a token is declared before it is being used,
- it cannot determine if a token is initialized before it is being used,
- it cannot determine if an operation performed on a token type is valid or not.
These tasks are accomplished by the semantic analyzer, which we shall study in Semantic Analysis.