All right, so you’ve read about sorting algorithms, and now you’ve got a sorted array. Just having a sorted array, however, doesn’t do anything for you unless you are going to search for things in the array itself.

Assume you have a sorted array. Now, when you search for that item, what you really want to do is see if the item is actually stored in the array. If it isn’t, then you want the algorithm to say so. If the item actually is present, however, then you want the algorithm to not only say that it is present, but you also want to have the algorithm return the entire element so that you can access it.

Now, let’s say that the elements of your sorted array are records of employees, sorted by the employee’s 3-digit company ID number (this is a small company, so the number is – we can hope – unique to each employee). Now, we want to see if an employee with a certain ID number – 243, for instance – exists. Let’s call that number the target number.

There are a variety of algorithms to search a sorted array, but we shall examine only two of them. One is extremely simple, and the other one is still relatively easy, but it is greatly more efficient.

The simplest way is to just start at the beginning of the array and compare, from smallest to greatest, each employee’s ID number with the target number. When the target number becomes smaller than an employee’s ID number, then we know that the target number isn’t in the array. This is called the linear search method.

Of course, if the target number were really big, then we’d have to compare it to almost every single element in the array before deciding whether or not it is in the array, and that’s slow.

The linear search method works well for arrays with which you can only access the elements of the array in order that they come; this kind of array is called a stream, and you often use this method with ordered linked lists, where you have to start at the beginning and just compare down the entire linked list.

For normal arrays, however, there is a more efficient method. This algorithm relies upon the fact that you can access any element of the array without having to go through all of the elements before it; this ability is called random access. (On a side note, the temporary memory in your computer is basically a big array that you can access like this, and so it is called Random Access Memory, or RAM.)

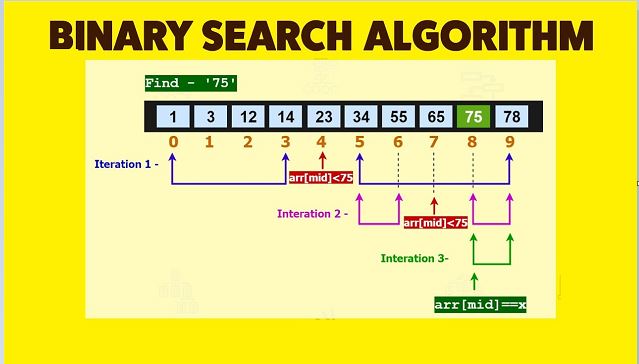
Let’s say our ordered array has 100 employees recorded in it. Since we can access any array element we want, and since the array elements are in order, wouldn’t it be more efficient to start searching in the middle of the array? That way, if the target number is less than the middle employee’s ID number, then we know that all of the numbers coming after this employee’s ID are going to be bigger than the target number anyway. If the target’s bigger, than the situation is just the opposite. So, we can eliminate half the array from the search!

Now, we’re down to one section of the array. We could search this section with the linear method…or we could just treat it as another array and start from the middle again. Now, we can do this over and over until we either find an element that matches the target number, or we’re down to a section with only one element in it that doesn’t match the target number. So, we’ve got the results we wanted, and the algorithm is much faster than just searching from one end. This method is called the binary search algorithm, because you keep on dividing the array into two halves. It is also known as the Divide-and-Conquer search algorithm

For the people knowledgeable about Big-O notation and mathematics, this algorithm is essentially O(log2(n)). That is, this algorithm has the order-of-magnitude similar to the logarithm of n to the base 2, where n is the number of elements in the sorted array.

What does this mean in non-mathematical terms? Well, if you have a sorted array of one thousand elements, using the first searching method, you might search all of the elements, making up to 1000 comparisons in the worst case. With the second method, however, you will make at most about 10 comparisons. The time saved gets even better when you get to talking about extremely large numbers: for a huge array of 1 trillion elements (American trillion, that is, which is numerically 1,000,000,000,000), using the second method, you only have to make up to 40 comparisons!! That’s all!

The way you implement the binary search algorithm is really quite simple. You need two variables: a low variable (usually named lo) and a high variable (usually named hi), which keep track of the beginning and the end of the section of the array that you are looking at. Initially, lo will store the index value of the first element of the array (in C++, that is normally 0), and hi will store the index value of the last element of the array (in C++, that would be n-1, where n is the number of elements).

You need to find the middle of the section. The index for the middle element is basically (hi – lo)/2 + lo rounded off to the nearest integer in some manner. If t (the target number) is less than the middle element, then reset hi to equal that middle element’s index. If t is greater than the middle element, then reset lo to equal the middle element’s index instead. That means that in the next round, we will only look at the elements with index numbers greater than lo and less than hi. In this way, you will eventually narrow down on where the target number should be in the array.

This handy little algorithm has been used everywhere, and it has even been modified to be used in a Chess playing algorithm called MTD(f). So, have fun with this new, time-saving search algorithm. It is easy to program, since essentially the algorithm is a loop that keeps going until lo and hi are overlapping. In each loop, the algorithm should check for three cases and act accordingly: if the target is equal to the middle element, if the target is less than the middle element, or if the target is greater.