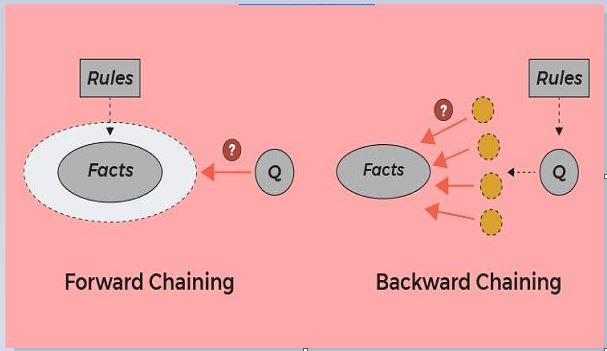
Backward-chaining is also known as a backward deduction or backward reasoning method when using an inference engine. A backward chaining algorithm is a form of reasoning, which starts with the goal and works backward, chaining through rules to find known facts that support the goal.

Properties of backward chaining:

• It is known as a top-down approach.
• Backward-chaining is based on modus ponens inference rule.
• In backward chaining, the goal is broken into sub-goal or sub-goals to prove the facts true.
• It is called a goal-driven approach, as a list of goals decides which rules are selected and used.
• Backward -chaining algorithm is used in game theory, automated theorem proving tools, inference engines, proof assistants, and various AI applications.
• The backward-chaining method mostly used a depth-first search strategy for proof.

Example:

In backward-chaining, we will use the same above example, and will rewrite all the rules.

• American (p) ∧ weapon(q) ∧ sells (p, q, r) ∧ hostile(r) → Criminal(p) …(1)
  Owns(A, T1)                 ……..(2)
• Missile(T1)
• ?p Missiles(p) ∧ Owns (A, p) → Sells (Robert, p, A)           ……(4)
• Missile(p) → Weapons (p)                 …….(5)
• Enemy(p, America) →Hostile(p)                 ……..(6)
• Enemy (A, America)                 ………(7)
• American(Robert).                 ……….(8)

Backward-Chaining proof:

In Backward chaining, we will start with our goal predicate, which is Criminal(Robert), and then infer further rules.

Step-1:

At the first step, we will take the goal fact. And from the goal fact, we will infer other facts, and at last, we will prove those facts true. So our goal fact is “Robert is Criminal,” so following is the predicate of it.

Step-2:

At the second step, we will infer other facts form goal fact which satisfies the rules. So as we can see in Rule-1, the goal predicate Criminal (Robert) is present with substitution {Robert/P}. So we will add all the conjunctive facts below the first level and will replace p with Robert.

Here we can see American (Robert) is a fact, so it is proved here.

Step-3:t At step-3, we will extract further fact Missile(q) which infer from Weapon(q), as it satisfies Rule-(5). Weapon (q) is also true with the substitution of a constant T1 at q.

Step-4:

At step-4, we can infer facts Missile(T1) and Owns(A, T1) form Sells(Robert, T1, r) which satisfies the Rule- 4, with the substitution of A in place of r. So these two statements are proved here.

Step-5:

At step-5, we can infer the fact Enemy(A, America) from Hostile(A) which satisfies Rule- 6. And hence all the statements are proved true using backward chaining.