The agents we have constructed so far have beliefs and can deduce new beliefs. Yet none of them has any knowledge about beliefs or about deduction. Knowledge about one’s own knowledge and reasoning processes is useful for controlling inference

propositional attitudes – the attitude an agent has towards mental objects (e.g. Believes, Knows, Wants, Intends, and Informs). These propositional attitudes do not behave like normal predicates

for example, to assert that Lois knows that Superman can fly:

one issue, is that if “Superman is Clark Kent is true“, then the inferential rules concludes that “Lois knows that Clark can fly” (this is an example of referential transparency). But in reality Lois doesn’t actually know that clark can fly

referential transparency

§  an expression always evaluates to the same result in any context

§  e.g. if agent knows that 2+2=4 and 4<5, then agent should know that 2+2<5

§  built into inferential rules of most formal logic languages

referential opacity

§  not referential transparent

§  we want referential opacity for propositional attitudes because terms do matter and not all agents know which terms are co-referential

§  not directly possible in most formal logic languages (except Modal Logic)

Modal Logic

designed to allow referential opacity into knowledge base.

regular logic is concerned with single modality (the modality of truth), allowing us to express “P is true”

modal logic includes modal operators that takes sentences (rather than terms) as arguments (e.g. “A knows P” is represented with notation K_AP where K is the modal operator for knowledge, _A is the agent, and P is a sentence).

syntax of modal logic is the same as first-order logic, with the addition that sentences can also be formed with modal operators

semantics of modal logic is more complicated. In first-order logic a model contains a set of objects and an interpretation that maps each name to the appropriate object, relation, or function. In modal logic we want to be able to consider both the possibility that Superman’s secret identity is Clark and that it isn’t. Therefore, in modal logic a model consists of a collection of possible worlds (instead of 1 true world). The worlds are connected in a graph by accessibility relations (one relation for each modal operator). We say that world w₁ is accessible from world w₀ with respect to the modal operator K_A if everything in w₁ is consistent with what A knows in w₀, and we write this as Acc(K_A, w₀, w₁)

Figure 12.4 shows accessibility as an arrow between possible worlds

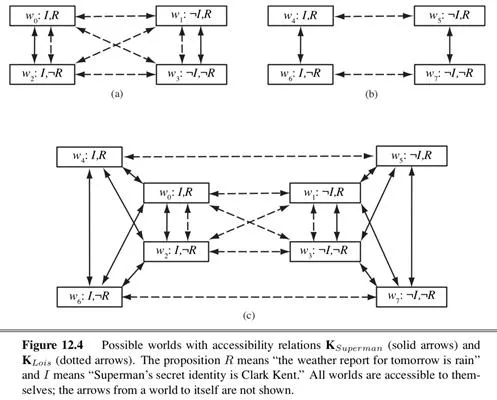
A knowledge atom K_AP is true in world w if and only if P is true in every world accessible from w. The truth of more complex sentences is derived by recursive application of this rule and the normal rules of first-order logic. That means that modal logic can be used to reason about nested knowledge sentences: what one agent knows about another agent’s knowledge.

For example, we can say that, even though Lois doesn’t know whether Superman’s secret identity is Clark Kent, she does know that Clark knows:

K_Lois[K_Clark Identity(Superman, Clark) ∨ K_Clark ¬Identity(Superman, Clark)]

In TOP-LEFT of figure 12.4 we represent the scenario where it is common knowledge that Superman knows his own identity, and neither he nor Lois has seen the weather report. So in w0 the worlds w0 and w2 are accessible to Superman; maybe rain is predicted, maybe not. For Lois all four worlds are accessible from each other; she doesn’t know anything about the report or if Clark is Superman. But she does know that Superman knows whether he is Clark, because in every world that is accessible to Lois, either Superman knows I, or he knows ¬I. Lois does not know which is the case, but either way she knows Superman knows.

In the TOP-RIGHT of figure 12.4 we represent the scenario where it is common knowledge that Lois has seen the weather report. So in w4 she knows rain is predicted and in w6 she knows rain is not predicted. Superman does not know the report, but he knows that Lois knows, because in every world that is accessible to him, either she knows R or she knows ¬R.

In the BOTTOM of figure 12.4 we represent the scenario where it is common knowledge that Superman knows his identity, and Lois might or might not have seen the weather report. We represent this by combining the two top scenarios, and adding arrows to show that Superman does not know which scenario actually holds. Lois does know, so we don’t need to add any arrows for her. In w0 Superman still knows I but not R, and now he does not know whether Lois knows R. From what Superman knows, he might be in w0 or w2, in which case Lois does not know whether R is true, or he could be in w4, in which case she knows R, or w6, in which case she knows ¬R.