It can be viewed as an attempt to find a left-most derivation for an input string or an attempt to construct a parse tree for the input starting from the root to the leaves.
Types -downoftopparsing :
1. Recursive descent parsing
2. Predictive parsing
RECURSIVE DESCENT PARSING
Typically, top-down parsers are implemented as a set of recursive functions that descent through a parse tree for a string. This approach is known as recursive descent parsing, also known as LL(k) parsing where the first L stands for left-to-right, the second L stands for leftmost-derivation, and k indicates k-symbol lookahead.
Therefore, a parser using the single-symbol look-ahead method and top-down parsing without backtracking is called LL(1) parser. In the following sections, we will also use an extended BNF notation in which some regulation expression operators are to be incorporated.
This parsing method may involve backtracking.
Example for :backtracking
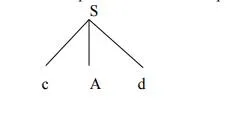
Consider the grammar G : S → cAd
A→ab|a
and the input string w=cad.
The parse tree can be constructed using the following top-down approach :
Step1:
Initially create a tree with single node labeled S. An input pointer points to ‘c’, the first symbol of w. Expand the tree with the production of S.
Step2:
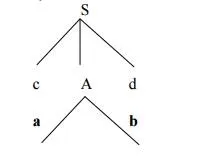
The leftmost leaf ‘c’ matches the first symbol of w, so advance the input pointer to the second symbol of w ‘a’ and consider the next leaf ‘A’. Expand A using the first alternative.
Step3:
The second symbol ‘a’ of w also matches with second leaf of tree. So advance the input pointer to third symbol of w ‘d’.But the third leaf of tree is b which does not match with the input symbol d.Hence discard the chosen production and reset the pointer to second backtracking.
Step4:
Now try the second alternative for A.
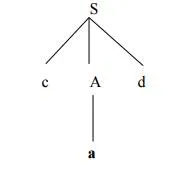
Now we can halt and announce the successful completion of parsing.
Predictive parsing
It is possible to build a nonrecursive predictive parser by maintaining a stack explicitly, rather than implicitly via recursive calls. The key problem during predictive parsing is that of determining the production to be applied for a nonterminal . The nonrecursive parser in figure looks up the production to be applied in parsing table. In what follows, we shall see how the table can be constructed directly from certain grammars.
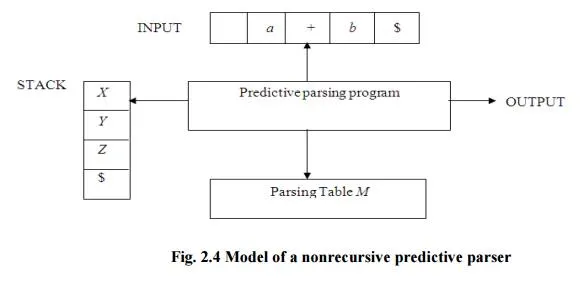
Fig. 2.4 Model of a nonrecursive predictive parser
A table-driven predictive parser has an input buffer, a stack, a parsing table, and an output stream. The input buffer contains the string to be parsed, followed by $, a symbol used as a right endmarker to indicate the end of the input string. The stack contains a sequence of grammar symbols with $ on the bottom, indicating the bottom of the stack. Initially, the stack contains the start symbol of the grammar on top of $. The parsing table is a two dimensional array M[A,a] where A is a nonterminal, and a is a terminal or the symbol $. The parser is controlled by a program that behaves as follows. The program considers X, the symbol on the top of the stack, and a, the current input symbol. These two symbols determine the action of the parser. There are three possibilities.
1 If X= a=$, the parser halts and announces successful completion of parsing.
2 If X=a!=$, the parser pops X off the stack and advances the input pointer to the next input symbol.
3 If X is a nonterminal, the program consults entry M[X,a] of the parsing table M. This entry will be either an X-production of the grammar or an error entry. If, for example, M[X,a]={X- >UVW}, the parser replaces X on top of the stack by WVU( with U on top). As output, we shall assume that the parser just prints the production used; any other code could be executed here. If M[X,a]=error, the parser calls an error recovery routine
Algorithm for Nonrecursive predictive arsing.
Input. A string w and a parsing table M for grammar G.
Output. If w is in L(G), a leftmost derivation of w; otherwise, an error indication.
Method. Initially, the parser is in a configuration in which it has $S on the stack with S, the start symbol of G on top, and w$ in the input buffer. The program that utilizes the predictive parsing table M to produce a parse for the input is shown in Fig.
set ip to point to the first symbol of w$. repeat
let X be the top stack symbol and a the symbol pointed to by ip. if X is a terminal of $ then
if X=a then
pop X from the stack and advance ip else error()
else
if M[X,a]=X->Y1Y2…Yk then begin pop X from the stack;
push Yk,Yk-1…Y1 onto the stack, with Y1 on top; output the production X-> Y1Y2…Yk
end
else error()
until X=$ /* stack is empty */
Predictive parsing table construction:
The construction of a predictive parser is aided by two functions associated with a grammar G :
3. FIRST
4. FOLLOW
Rules for first( ):
1. If X is terminal, then FIRST(X) is {X}.
2. If X → ε is a production, then add ε to FIRST(X).
3. If X is non-terminal and X → aα is a production then add a to FIRST(X).
4. If X is non-terminal and X → Y1 Y2…Yk is a production, then place a in FIRST(X) if for some i, a is in FIRST(Yi), and ε is in all of FIRST(Y1),…,FIRST(Yi-1);that is, Y1,….Yi-1=> ε. If ε is in FIRST(Yj) for all j=1,2,..,k, then add ε to FIRST(X).
Rules for follow( ):
1. If S is a start symbol, then FOLLOW(S) contains $.
2. If there is a production A → αBβ, then everything in FIRST(β) except ε is placed in
follow(B).
3. If there is a production A → αB, or a production A → αBβ where FIRST(β) contains
ε, then everything in FOLLOW(A) is in FOLLOW(B).
Algorithm for construction of predictive parsing table:
Input : Grammar G
Output : Parsing table M
Method :
1. For each production A → α of the grammar, do steps 2 and 3.
2. For each terminal a in FIRST(α), add A → α to M[A, a].
3. If ε is in FIRST(α), add A → α to M[A, b] for each terminal b in FOLLOW(A). If ε is in FIRST(α) and $ is in FOLLOW(A) , add A → α to M[A, $].
4. Make each undefined entry of M be error.
Example:
Consider the following grammar :
E→E+T|T
T→T*F|F
F→(E)|id
After eliminating left-recursion the grammar is
E →TE’
E’ → +TE’ | ε
T →FT’
T’ → *FT’ | ε
F → (E)|id
First( ) :
FIRST(E) = { ( , id}
FIRST(E’) ={+ , ε }
FIRST(T) = { ( , id}
FIRST(T’) = {*, ε }
FIRST(F) = { ( , id }
Follow( ):
FOLLOW(E) = { $, ) }
FOLLOW(E’) = { $, ) }
FOLLOW(T) = { +, $, ) }
FOLLOW(T’) = { +, $, ) }
FOLLOW(F) = {+, * , $ , ) }
Predictive parsing Table

Stack Implementation
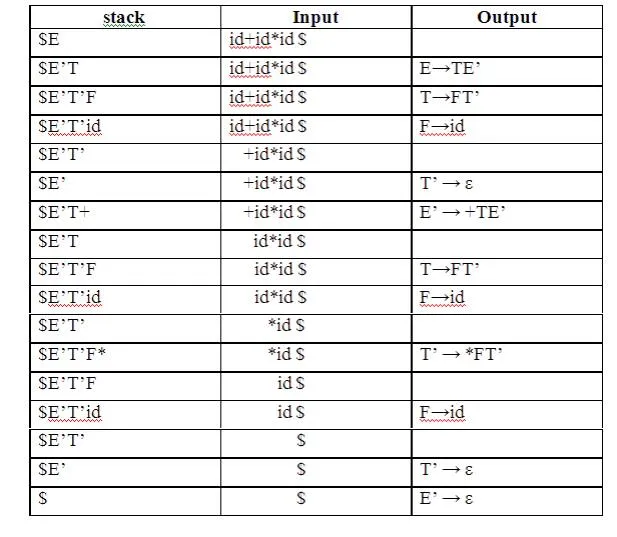
LL(1) grammar:
The parsing table entries are single entries. So each location has not more than one entry. This type of grammar is called LL(1) grammar.
Consider this following grammar:
S→iEtS | iEtSeS| a
E→b
After eliminating left factoring, we have
S→iEtSS’|a
S’→ eS | ε
E→b
To construct a parsing table, we need FIRST() and FOLLOW() for all the non-terminals.
FIRST(S) = { i, a }
FIRST(S’) = {e, ε }
FIRST(E) = { b}
FOLLOW(S) = { $ ,e }
FOLLOW(S’) = { $ ,e }
FOLLOW(E) = {t}
Parsing table:
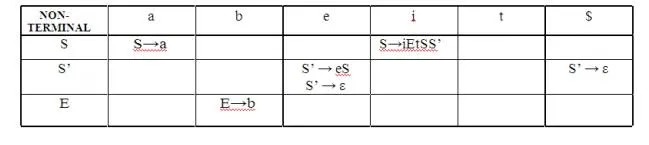
Since there are more than one production, the grammar is not LL(1) grammar.
Actions performed in predictive parsing:
1. Shift
2. Reduce
3. Accept
4. Error
Implementation of predictive parser:
1. Elimination of left recursion, left factoring and ambiguous grammar.
2. Construct FIRST() and FOLLOW() for all non-terminals.
3. Construct predictive parsing table.
4. Parse the given input string using stack and parsing table