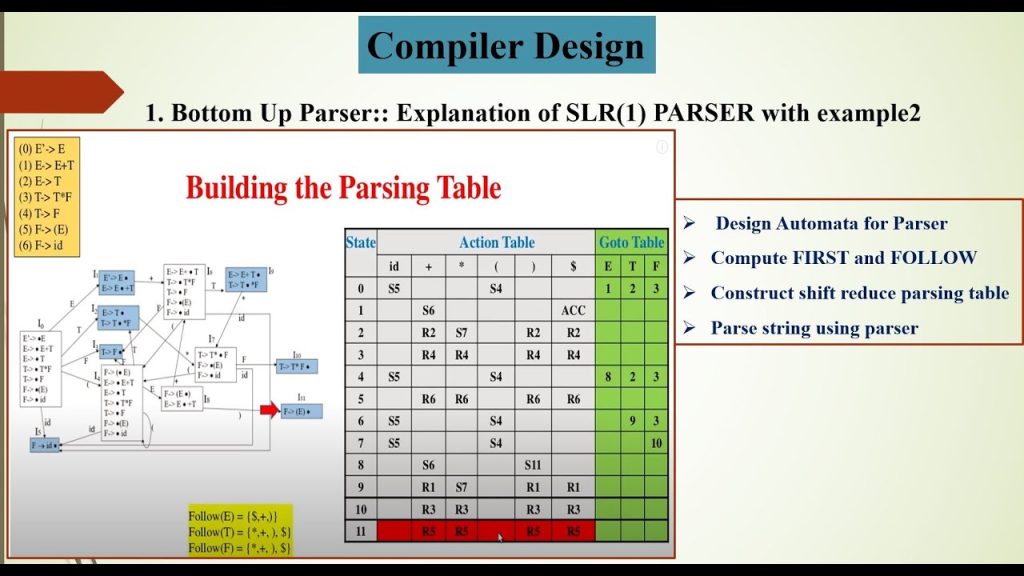
Constructing a parse tree for an input string beginning at the leaves and going towards the root is called bottom-up parsing. A general type of bottom-up parser is a shift-reduce parser.
SHIFT-REDUCE PARSING
Shift-reduce parsing is a type of bottom-up parsing that attempts to construct a parse tree for an input string beginning at the leaves (the bottom) and working up towards the root (the top).
Example:
Consider the grammar:
S → aABe
A → Abc | b
B → d
The sentence to be recognized is abbcde.
REDUCTION (LEFTMOST) RIGHTMOST DERIVATION
abbcde (A → b) S → aABe
aAbcde(A → Abc) → aAde
aAde (B → d) → aAbcde
aABe (S → aABe) → abbcde
S
The reductions trace out the right-most derivation in reverse.
Handles:
A handle of a string is a substring that matches the right side of a production, and whose reduction to the non-terminal on the left side of the production represents one step along the reverse of a rightmost derivation.
Example:
Consider the grammar:
E→E+E
E→E*E
E→(E)
E→id
And the input string id1+id2*id3
The rightmost derivation is :
E→E+E
→ E+E*E
→ E+E*id3
→ E+id2*id3
→ id1+id2*
In the above derivation the underlined substrings are called handles.
Handle pruning:
A rightmost derivation in reverse can be obtained by “handle pruning”. (i.e.) if w is a sentence or string of the grammar at hand, then w = γn, where γn is the nth rightsentinel form of
some rightmost derivation.
Actions in shift-reduce parser:
• shift – The next input symbol is shifted onto the top of the stack.
• reduce – The parser replaces the handle within a stack with a non-terminal.
• accept – The parser announces successful completion of parsing.
• error – The parser discovers that a syntax error has occurred and calls an error recovery routine.
Conflicts in shift-reduce parsing:
There are two conflicts that occur in shift-reduce parsing:
1. Shift-reduce conflict: The parser cannot decide whether to shift or to reduce.
2. Reduce-reduce conflict: The parser cannot decide which of several reductions to make.
Stack implementation of shift-reduce parsing :

1. Shift-reduce conflict:
Example:
Consider the grammar:
E→E+E | E*E | id and input id+id*id

2. Reduce-reduce conflict:
Consider the grammar: M→R+R|R+c|R
R→c
and input c+c

Viable prefixes:
α is a viable prefix of the grammar if there is w such that αw is a right
The set of prefixes of right sentinel forms that can appear on the stack of a shift-reduce parser are called viable prefixes
The set of viable prefixes is a regular language.
OPERATOR-PRECEDENCE PARSING
An efficient way of constructing shift-reduce parser is called operator-precedence parsing. Operator precedence parser can be constructed from a grammar called Operator-grammar. These grammars have the property that no production on right side is ɛor has two adjacent non-terminals.
Example:
Consider the grammar:
E→EAE|(E)|-E|id
A→+|-|*|/|↑
Since the right side EAE has three consecutive non-terminals, the grammar can be written as follows: E→E+E|E-E|E*E|E/E|E↑E |-E|id
Operator precedence relations:
There are three disjoint precedence relations namely
<. – less than
= – equal to
.> – greater than
The relations give the following meaning:
a<.b – a yields precedence to b
a=b – a has the same precedence as b
a.>b – a takes precedence over b
Rules for binary operations:
1. If operator θ1 has higher precedence than operator θ2, then make
θ1 . > θ2 and θ2 < . θ1
2. If operators θ1 and θ2, are of equal precedence, then make
θ1 . > θ2 and θ2 . > θ1 if operators are left associative
θ1 < . θ2 and θ2 < . θ1 if right associative
3. Make the following for all operators θ:
θ <. id ,id.>θ
θ <.(, (<.θ
).>θ, θ.>)
θ.>$ , $<. θ
Also make
( = ) , ( <. ( , ) .> ) , (<. id, id .>) , $ <. id , id .> $ , $ Example:
Operator-precedence relations for the grammar
E→E+E|E-E|E*E|E/E|E↑E |(E)|-E|idis given in the following table assuming
1. ↑ is of highest precedence and right-associative
2. * and / are of next higher precedence and left-associative, and
3. + and – are of lowest precedence and left- Note that the blanks in the table denote error entries.
Table : Operator-precedence relations

Operator precedence parsing algorithm:
Input : An input string w and a table of precedence relations.
Output : If w is well formed, a skeletal parse tree ,with a placeholder non-terminal E labeling all interior nodes; otherwise, an error indication.
Method : Initially the stack contains $ and the input buffer the string w $. To parse, we execute the following program :
(1) Set ip to point to the first symbol of w$;
(2) repeat forever
(3) if $ is on top of the stack and ip points to $ then
(4) return else begin
(5) let a be the topmost terminal symbol on the stack and let b be the symbol pointed to by ip;
(6) if a <. b or a = b then begin
(7) push b onto the stack;
(8) advance ip to the next input symbol; end;
(9) else if a . > b then /*reduce*/
(10) repeat
(11) pop the stack
(12) until the top stack terminal is related by <.to the terminal most recently popped
(13) else error( ) end
Stack implementation of operator precedence parsing:
Operator precedence parsing uses a stack and precedence relation table for its implementation of above algorithm. It is a shift-reduce parsing containing all four actions shift, reduce, accept and error.
The initial configuration of an operator precedence parsing is
STACK : $
INPUT : w$
where w is the input string to be parsed.
Example:
Consider the grammar E → E+E | E-E | E*E | E/E | E↑E | (E) | id. Input string is id+id*id .The implementation is as follows:

Advantages of operator precedence parsing:
1. It is easy to implement.
2. Once an operator precedence relation is made between all pairs of terminals of a grammar, the grammar can be ignored. The grammar is not referred anymore during implementation.
Disadvantages of operator precedence parsing:
1. It is hard to handle tokens like the minus sign (-) which has two different precedence.
2. Only a small class of grammar can be parsed using operator-precedence parser.