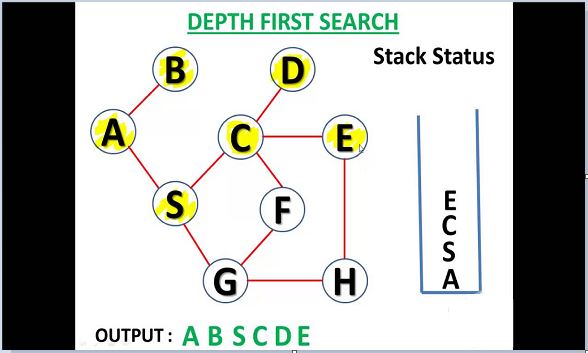
Depth-first search (DFS) is an algorithm for traversing or searching tree or graph data structures. The algorithm starts at the root node (selecting some arbitrary node as the root node in the case of a graph) and explores as far as possible along each branch before backtracking.
Example:
Question. Which solution would DFS find to move from node S to node G if run on the graph below?
Solution. The equivalent search tree for the above graph is as follows. As DFS traverses the tree “deepest node first”, it would always pick the deeper branch until it reaches the solution (or it runs out of nodes, and goes to the next branch). The traversal is shown in blue arrows.
Path: S -> A -> B -> C -> G
Let ![]() = the depth of the search tree = number of levels of the search tree.
= the depth of the search tree = number of levels of the search tree.![]() = number of nodes in level
= number of nodes in level ![]() .
.
Time complexity: Equivalent to the number of nodes traversed in DFS. 
Space complexity: Equivalent to how large can the fringe get. 
Completeness: DFS is complete if the search tree is finite, meaning for a given finite search tree, DFS will come up with a solution if it exists.
Optimality: DFS is not optimal, meaning the number of steps in reaching the solution, or the cost spent in reaching it is high.
Breadth First Search
Breadth-first search (BFS) is an algorithm for traversing or searching tree or graph data structures. It starts at the tree root (or some arbitrary node of a graph, sometimes referred to as a ‘search key’), and explores all of the neighbor nodes at the present depth prior to moving on to the nodes at the next depth level.
Example:
Question. Which solution would BFS find to move from node S to node G if run on the graph below?
Solution. The equivalent search tree for the above graph is as follows. As BFS traverses the tree “shallowest node first”, it would always pick the shallower branch until it reaches the solution (or it runs out of nodes, and goes to the next branch). The traversal is shown in blue arrows.

Path: S -> D -> G
Let ![]() = the depth of the shallowest solution.
= the depth of the shallowest solution.![]() = number of nodes in level
= number of nodes in level ![]() .
.
Time complexity: Equivalent to the number of nodes traversed in BFS until the shallowest solution. 
Space complexity: Equivalent to how large can the fringe get. 
Completeness: BFS is complete, meaning for a given search tree, BFS will come up with a solution if it exists.
Optimality: BFS is optimal as long as the costs of all edges are equal


Comments are closed